A 45-45-90 triangle is a unique kind of isosceles right triangle. In this triangle, both legs are equal in length, and the non-right angles are both 45 degrees. This means that the hypotenuse, which is the longest side of the triangle, is equal to the length of one of the legs multiplied by the square root of 2. This property makes it easy to calculate the length of any side of the triangle if you know the length of one of the sides.
The 45-45-90 triangle is commonly used in geometry and trigonometry, and it has many practical applications in fields such as engineering and architecture.
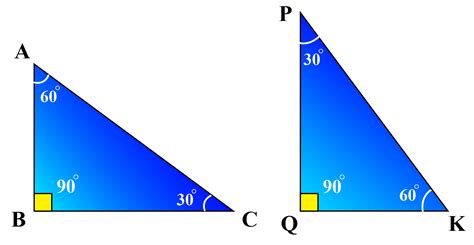
What is special about a 30-60-90 triangle?
A right triangle is a triangle that contains a 90 degree angle. One type of right triangle is the 30-60-90 triangle, which always has degree angles of 30 degrees, 60 degrees, and 90 degrees. This special triangle has side length values that are always in a consistent relationship with one another.
How do you know if a triangle is 30-60-90 or 45 45 90?
To determine if a triangle is a 30-60-90 or a 45-45-90 triangle, you need to look at the angles. In a 30-60-90 triangle, the angles are 30 degrees, 60 degrees, and 90 degrees. The side opposite the 30-degree angle is half the length of the hypotenuse, and the side opposite the 60-degree angle is √3 times the length of the side opposite the 30-degree angle. In a 45-45-90 triangle, the angles are both 45 degrees, and the sides are congruent.
The hypotenuse is √2 times the length of either leg. By knowing the angles or the side lengths,
What is the 30-60-90 triangle rule?
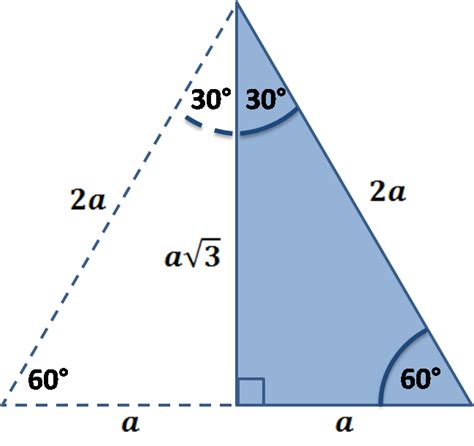
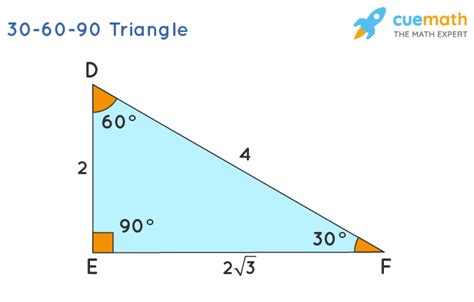
30-60-90 triangles are a type of right triangle where one angle measures 30 degrees, another measures 60 degrees, and the third angle is a right angle of 90 degrees. In this type of triangle, the hypotenuse, which is the side opposite the 60-degree angle, is twice the length of the shorter leg, which is the side opposite the 30-degree angle. The longer leg, which is the side opposite the 90-degree angle, is square root of 3 times the length of the shorter leg.
What is the 45 45 90 rule?
The Pythagorean theorem can be used to prove the 45-45-90 triangle rule, which is a useful geometric concept to know. This rule states that the three sides of the triangle are in the ratio 1:1:\(\sqrt{2}\). This means that if the measure of the two congruent sides of such a triangle is x each, then the three sides will be x, x and \(\sqrt{2}x\). Understanding this rule can help in solving problems related to right triangles and can be applied in various fields such as architecture, engineering, and physics.
What is the 30 60 90 theorem proof?
In a triangle, the length of each side is determined by the angle opposite to it. The smallest angle, which is 30 degrees, will always have the shortest side opposite to it. The medium length side will be opposite to the 60-degree angle, which is the mid-sized degree angle in the triangle. Finally, the largest angle, which is 90 degrees, will always have the longest side opposite to it.
This relationship between angles and side lengths is a fundamental concept in geometry and is essential for solving various mathematical problems involving triangles.
How do you prove a triangle is a right angle?
If you’re wondering whether a triangle has a right angle, Pythagoras’ theorem can help you figure it out. All you need to do is square the lengths of the two shorter sides and add them together. If the result is equal to the square of the length of the longest side (also known as the hypotenuse), then the triangle contains a right angle. This theorem has been used for centuries and is still widely used today in various fields of study, including mathematics, engineering, and physics.
What are the formulas for 45 45 90 and & 30 60 90 special right triangles?
The formulas for the 45 45 90 special right triangle are that the two legs are congruent and the hypotenuse is equal to the leg times the square root of 2. For the 30 60 90 special right triangle, the hypotenuse is twice the shorter leg, the longer leg is the shorter leg times the square root of 3, and the angles are 30, 60, and 90 degrees. These formulas can be useful in solving problems involving these special right triangles, which are commonly found in geometry and trigonometry.
Why are they special right triangles?
A right triangle that possesses a unique characteristic, making calculations on the triangle simpler or for which straightforward formulas exist, is known as a special right triangle. One example of this is an “angle-based” right triangle, which has angles that form uncomplicated relationships, such as 45°–45°–90°.
What makes 45-45-90 and 30-60-90 triangles special when solving for missing sides?
Special triangles, like the 30-60-90 and 45-45-90 triangles, have specific formulas for determining the length of their sides. These triangles have fixed internal angles, and their side values can be used as identities.
What is the special triangle rule?
A 45-45-90 triangle is a unique right triangle that has a specific ratio between the lengths of its sides. This ratio is always 1:1:√2, which means that if one leg of the triangle is x units long, then the other leg is also x units long, and the hypotenuse is x√2 units long. This property makes it easy to calculate the length of any side of the triangle if you know the length of one of the sides. It is a useful concept to understand in geometry and can be applied in various real-world situations, such as in construction or engineering.
What are the 5 Pythagorean triples?
Pythagorean triples are sets of three integers that satisfy the Pythagorean theorem, a² + b² = c². The most common Pythagorean triples are (3, 4, 5), (5, 12, 13), (6, 8, 10), (9, 12, 15), and (15, 20, 25). These triples have been studied for centuries and have many practical applications, such as in construction and engineering. They are also used in mathematics education to teach students about the Pythagorean theorem and its applications.
Understanding Pythagorean triples can be helpful in solving problems in geometry and trigonometry, and can also be a fun mathematical puzzle to explore.
What is the golden ratio right triangle?
The Golden Ratio, symbolized by the Greek letter Φ and equal to 1.61803…
, is incorporated into several well-known triangles known as the Golden Triangles. These triangles are named after the mathematical constant because of its significance in their design. The Golden Ratio has been studied extensively and has been found to have a pleasing aesthetic quality, which is why it is often used in art and architecture. Additionally, some researchers believe that the Golden Ratio may have a connection to the natural world and can be found in the proportions of many living organisms.
Is 8 10 6 a right triangle?
Therefore, it can be concluded that the triangle in question is indeed a right triangle. This can be determined by examining the lengths of its sides, which have been provided below.
Is 15 36 39 a right triangle?
Therefore, we can conclude that the triangle has a 90-degree angle, making it a right-angled triangle. This is an important property of triangles that can be used to solve various mathematical problems. The right angle divides the triangle into two smaller triangles, each with its own unique properties and measurements. Understanding the concept of right-angled triangles is essential in fields such as geometry, trigonometry, and engineering.
It is also a fundamental concept in everyday life, as right-angled triangles can be found in various objects and structures, from buildings to furniture.
Is 21 28 35 a right triangle?
Let’s now check if a triangle with sides measuring 21, 28, and 35 is a right triangle. By applying the Pythagorean Theorem, we can confirm that this triangle is indeed a right triangle. Therefore, the lengths of 21, 28, and 35 form a right triangle.
Is 9 40 41 a right triangle?
As a result of satisfying the Pythagoras theorem, the three sides 9, 40, and 41 can be considered as the sides of a right-angled triangle. This mathematical concept is crucial in understanding the relationship between the sides of a triangle and the angles they form. By applying this theorem, we can determine whether a triangle is a right-angled triangle or not. It is a fundamental concept in mathematics and has numerous applications in fields such as engineering, architecture, and physics.
How do you find the missing side of a triangle?
To find the missing side of a triangle, you need to use the Pythagorean theorem or trigonometric ratios depending on the information given. If you have two sides of a right triangle, you can use the Pythagorean theorem to find the missing side. If you have one side and an angle, you can use trigonometric ratios such as sine, cosine, or tangent to find the missing side. It’s important to remember to use the appropriate formula based on the given information and to label the sides and angles correctly.
Additionally, you can use a calculator or online tool to help with the calculations.
How do you find the area of a 30 60 90 right triangle?
To find the area of a 30-60-90 right triangle, you need to know the length of one of the sides. Let’s call the length of the shorter leg “x”. The longer leg will be “x√3” and the hypotenuse will be “2x”. To find the area, you can use the formula A = 1/2bh, where “b” is the base and “h” is the height.
In this case, the base is “x” and the height is “x√3/2”. Plugging these values into the formula, you get A = 1/2(x)(x√3/2) = x²√3/4.
What is the formula for the 90 triangle?
If you’re looking to solve for the length of a side in a right triangle, the Pythagorean Theorem is your go-to formula. It states that the sum of the squares of the two legs in a right triangle is equal to the square of the hypotenuse. In other words, a² + b² = c², where a and b are the lengths of the legs and c is the length of the hypotenuse. This formula is incredibly useful in a variety of fields, from construction to engineering to mathematics.
How to find the height of a triangle?
To find the height of a triangle, you need to know the length of the base and the area of the triangle. The formula for finding the area of a triangle is 1/2(base x height). Rearranging this formula, we can solve for the height by dividing both sides by the base and multiplying by 2. So, the formula for finding the height of a triangle is height = (2 x area) / base.
Once you have the area and base measurements, simply plug them into the formula to find the height. It’s important to note that the height of a triangle is perpendicular to the base, so make sure you measure from the base to the highest point of the triangle.
Related Article
- Why Did Sonny Shoot The Guy In A Bronx Tale?
- Why Did Shang Kings Have Questions Scratched On Oracle Bones?
- Why Did My Ex Unfollow Me On Instagram Months Later?
- Why Did My Ex Request To Follow Me On Instagram?
- Why Did Michelle Phillips Eat A Banana On Ed Sullivan?
- Why Did Mary Beth Evans Leave Days Of Our Lives?
- Why Did Joseph Want His Bones Taken Out Of Egypt?
- Why Did It Take 46 Years To Build The Temple?
- Why Did Industrialization Help Start Japan On An Imperialist Course?
- Why Did I Have A Dream Of Someone Hurting Me?