Tables are a popular way to showcase functions, where the input and output values are displayed in rows or columns. These values can either represent the entire relationship or just a few examples from a more comprehensive one. Using tables can help simplify complex relationships and make them easier to understand.
Why is a table not a function?
When it comes to functions, it’s important to keep in mind that each input value can only be assigned to one output value. This means that if you come across an x-value that has multiple y-values, the table is not representing a function. It’s crucial to understand this concept in order to accurately represent functions with tables. By following this rule, you can ensure that your tables accurately reflect the relationship between input and output values.
Does the graph represent a function Why or why not?
When it comes to understanding functions, one key concept is the vertical line test. This test helps determine whether a graph represents a function or not. If a vertical line intersects the graph at only one point, then the graph is a function. However, if a vertical line intersects the graph at two or more points, then the graph does not represent a function.
This is an important concept to keep in mind when working with functions and can help ensure accuracy in mathematical calculations.
What is a function as a table?
A function table is a table that shows which coordinates should be plotted in the coordinate system, so that you can draw the graph of the function.
How do you tell if it is a function or not?
When analyzing a graph to determine if it represents a function, we can use the Vertical Line Test. This test is simple: draw a vertical line on the graph and observe how many times it intersects with the graph. If the line only intersects the graph once, then the graph represents a function. This is a useful tool for understanding the relationship between variables and ensuring that a graph accurately represents that relationship.
How do you write a function to represent a table?
To write a function to represent a table, you first need to determine the structure of the table. This includes the number of columns and rows, as well as the data types for each column. Once you have this information, you can create a function that takes in the necessary parameters and generates the table. This function should use HTML or another markup language to format the table and display the data in a clear and organized manner.
You may also want to include options for sorting or filtering the data, depending on the needs of your users. It’s important to thoroughly test your function to ensure that it works as expected and can handle a variety of inputs and scenarios.
How do we represent a function?
There are various ways to represent functions, including tables, symbols, and graphs, each with its own benefits. Tables provide a clear and explicit display of the functional values for specific inputs. On the other hand, symbolic representation offers a more concise way of computing functional values. By using symbols, complex functions can be expressed in a simpler and more manageable form.
Lastly, graphs provide a visual representation of the function, allowing for a better understanding of its behavior and patterns. Depending on the situation, each of these representations can be useful in conveying the information needed.
How do you tell what type of function a table is?
To determine the type of function a table represents, you need to analyze the pattern of the data. If the data points form a straight line, the function is linear. If the data points form a curve, the function is nonlinear. You can also look at the rate of change between the data points to determine if the function is increasing or decreasing.
Additionally, you can calculate the slope of the line or the curvature of the curve to determine the degree of the function. It’s important to note that not all functions can be easily identified from a table, and sometimes additional information or data points may be needed to accurately determine the function type.
What is an example of a function?
A basic illustration of a function is f(x) = x2. This function takes the input value of “x” and squares it. For instance, if x = 3, then f(3) = 9. Other examples of functions include f(x) = sin x, f(x) = x2 + 3, f(x) = 1/x, f(x) = 2x + 3, and so on.
What is a function vs not a function?
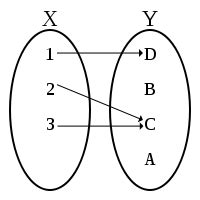
A function is a type of relation where each input corresponds to only one output. For instance, in the relation y = f(x), y is a function of x since every input x (such as 1, 2, 3, or 0) has only one output y. However, x is not a function of y because the input y = 3 has multiple outputs, namely x = 1 and x = 2. This concept is crucial in mathematics and has numerous applications in fields such as physics, engineering, and economics.
Understanding functions is essential for solving problems involving variables and their relationships.
What are the 4 types of functions?
Polynomial functions are a fundamental concept in mathematics, and they come in various degrees. A constant function is a polynomial function of degree zero, while a linear function is a polynomial function of degree one. Quadratic functions are polynomial functions of degree two, and cubic functions are polynomial functions of degree three. Understanding these different types of polynomial functions is essential in solving mathematical problems and modeling real-world situations.
What is not a function in math?
In math, there are certain terms that are often confused with functions. One of these is an equation, which is a statement that two expressions are equal. An equation can be solved for a variable, but it is not a function. Another term that is not a function is a relation, which is a set of ordered pairs that relate two variables.
While a relation can be graphed, it is not necessarily a function because it may fail the vertical line test. Additionally, a constant is not a function because it does not vary with the input. A function, on the other hand, is a rule that assigns a unique output to each input.
Which example is not a function?
Triple-delimited paragraph:
“`Many students struggle with understanding the concept of functions in mathematics. One common mistake is assuming that vertical lines are functions. However, this is not the case. Equations such as y = ± x and x 2 + y 2 = 9 are examples of non-functions because they have at least one -value with two or more -values.
To determine if a graph represents a function, we can use the vertical line test. This test involves drawing a vertical line through the graph. If the line intersects the graph at more than one point, then the graph is not a function. The vertical line test is a simple and effective way to visualize a violation of the definition of a function.
“`
What tables don’t represent a function?
“`When a specific x value has more than one y value, a table is not considered a function. This can be illustrated with an example where an x value of 11 appears twice in a table. The first instance of x=11 has a corresponding y value of 20, while the second instance of x=11 has a different y value of 16. In such cases, the table fails to meet the criteria of a function.
“`
What are the 5 ways of representing a function?
There are various ways to represent a function, including through a graph, table, symbols, words, and picture/context. However, a recursive relationship can also be used to represent the slope of the line in the equation. This means that the equation can be expressed in terms of itself, allowing for a more dynamic and flexible representation of the function. By understanding the different ways to represent a function, individuals can gain a deeper understanding of its behavior and make more informed decisions when working with mathematical concepts.
What is a function in a graph table?
A function in a graph table is a mathematical relationship between two sets of numbers, where each input value (x) corresponds to exactly one output value (y). In other words, for every x-value, there is only one y-value. This relationship can be represented graphically as a line or curve on a coordinate plane. The graph table displays the x and y values for each point on the graph.
Functions are used in many areas of mathematics, science, and engineering to model real-world phenomena and make predictions. Understanding functions and their graphs is essential for solving problems in these fields.
What is an example of a function?
A basic illustration of a function is f(x) = x2. This function takes the input value of “x” and squares it. For instance, if x = 3, then f(3) = 9. There are numerous other examples of functions, such as f(x) = sin x, f(x) = x2 + 3, f(x) = 1/x, f(x) = 2x + 3, and so on.
How can you tell what kind of function it is of of a table?
To determine the type of function represented by a table, you need to analyze the pattern of the data. If the data points form a straight line, the function is linear. If the data points form a curve, the function is nonlinear. You can also look at the rate of change between the data points.
If the rate of change is constant, the function is linear. If the rate of change varies, the function is nonlinear. Additionally, you can use calculus to find the derivative of the function and determine its slope at any point. This can help you identify whether the function is increasing or decreasing, and whether it has any maximum or minimum points.
What makes something a function?
A function is a type of relation where each input corresponds to only one output. For instance, in the relation y = f(x), y is a function of x since every input x (such as 1, 2, 3, or 0) has only one output y. However, x is not a function of y because the input y = 3 has multiple outputs, namely x = 1 and x = 2. This concept is crucial in mathematics and has numerous applications in fields such as physics, engineering, and economics.
Understanding functions is essential for solving problems involving variables and their relationships.
Related Article
- Why Would You Create A Statement Charge For A Customer?
- Why Would This Be Considered An Example Of Expository Writing?
- Why Would A Nursing Diagnosis Of A Cough Be Incorrect?
- Why Was The Use Of Credit Uncommon Prior To 1917?
- Why Was The Berlin Wall Called A Canvas Of Concrete?
- Why Was God Not In The Wind Earthquake And Fire?
- Why The Hell Are You Here Teacher Uncensored Episode 7?
- Why Put A Bread Clip In Your Wallet When Traveling?
- Why Isn’T John Lithgow Doing The Progresso Soup Commercials Anymore?
- Why Is Tom In A Coma In Ginny And Georgia?